Übung 8

Nun wollen wir diesen Zufallszahlengenerator random nutzen um eine Funktion zu entwickeln, welche einen beliebigen Punkt (mit einer x-/y-Koordinate) zufällig in einem definierten Umkreis verschiebt. Unser Fernziel ist es, den simulierten Datensatz aus “Datenqualität und Unsicherheit” zu rekonstruieren (siehe unten). Der erste Schritt dorthin ist es, einen gemeldeten Punkt (rot in Abbildung 29.1) in einem definierten Umkreis zu verschieben.

Abbildung 29.1: Ausschnitt der simulierten Zeckenstiche. Der rote Punkt stellt jeweils den gemeldeten Zeckenstich dar, die blaue Punktwolke drum herum sind simulierte Punkte welche die Ungenauigkeit der Daten wiederspiegelt.

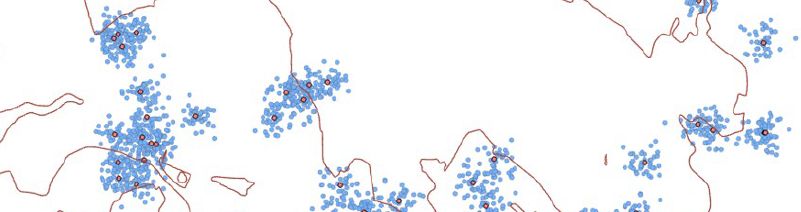
Das Ziel dieser Übung ist es also, dass wir eine Funktion entwickeln, die uns einen zufälligen Punkt in der Nähe eines Ursprungspunktes vorschlägt. Unser Vorgehen: Wir addieren jedem Koordinatenwert (x/y) des Ursprungspunktes einen Zufallswert, zum Beispiel zwischen -100 bis +100.

Übung 8.1

Bevor wir mit Koordinaten arbeiten wollt ihr euch zuerst mit dem Modul random vertraut machen. Importiere das Modul random und generiere eine Zufallszahl zwischen -100 und +100 aus einer uniformen Verteilung sowie aus einer Normalverteilung mit Mittelwert 100 und Standartabweichung 20.

import random

random.uniform(-100, 100)

random.normalvariate(100, 20)

Übung 8.2

Nun wollen wir uns den Koordinaten zuwenden. Erstelle als erstes zwei Dummykoordinaten x_start und y_start mit jeweils dem Wert 0. Diese sollen als “Ursprungskoordinaten” dienen.

x_start = 0
y_start = 0

Übung 8.3

Generiere nun eine Zufallszahl, die aus einer Normalverteilung stammt und die in etwa zwischen -100 und +100 liegt. Weise diese Zahl der Variabel x_offset zu. Generiere danach eine zweite Zufallszahl (auf die gleiche Art) und weise diese y_offset zu.

Hinweis

Überlege dir, welcher Mittelwert Sinn macht um Werte zwischen -100 und +100 zu bekommen. Welche Zahl liegt zwischen -100 und +100?

Überlege dir als nächstes, welche Standartabweichung sinnvoll wäre. Zur Erinnerung: Etwa 68% der Werte liegen inerhalb von +/- 1 Standartabweichung (SD), 95% innerhalb von +/- 2 SD, 99% innerhalb von 3 SD (siehe unten):

Abbildung 29.2: Normalverteilung und die Anteile innerhalb von 1 Standartabweichung (Mittelwert \(\mu\) minus Standartabweichung \(\sigma\)), 2 Standartabweichungen (\(\mu - 2\times\sigma)\) und 2 Standartabweichungen (\(\mu - 3\times\sigma)\). Quelle: cobocards

# Normalverteilte Werte mit Mittelwert 0 und Standartabweichung 100  
# Achtung: bei dieser Standartabweichung sind ca 30% der Werte > 100!
x_offset = random.normalvariate(0, 100)
y_offset = random.normalvariate(0, 100)

x_offset
y_offset

Übung 8.4

Addiere nun die Zufallszahlen x_offset und y_offset jeweils zu den Dummykoordinaten x_start und y_start und weise diese neuen Koordinaten x_neu und y_neu zu. Die neuen Werte stellen die leicht verschobenen Ursprungskoordinaten dar. In meinem Fall sind diese um 10.2 Meter nach Osten (positiver Wert) bzw. 4.4 Meter nach Süden (negativer Wert) verschoben worden.

x_offset = 10.246170309600945
y_offset = -4.443904000288846

x_neu = x_start + x_offset
y_neu = y_start + y_offset

x_neu

10.246170309600945

y_neu

-4.443904000288846

import pandas as pd

mypoints = pd.DataFrame({
    "x": [x_start, x_neu],
    "y": [y_start, y_neu],
    "typ": ["start", "neu"]
    }
)

from matplotlib import pyplot as plt

mypoints.plot("x", "y", kind = "scatter", xlim = [-100, 100], ylim = [-100, 100], c = ["red", "blue"], title = "Ursprung (rot) und Simulation (blau)")

ModuleNotFoundError: No module named 'pandas'

Übung 8.5

Nun haben wir das zufällige Verschieben eines Einzelpunktes am Beispiel einer Dummykoordinaten (0/0) durchgespielt. In der nächsten Aufgabe (Funktionen in DataFrames) werden wir alle unsere Zeckenstichkoordinaten auf diese Weise zufällig verschieben um einen simulierten Zeckenstichdatensatz ähnlich wie Abbildung 29.1 zu erhalten.

Dafür brauchen wir die eben erarbeiteten Einzelschritte als Funktion, um diese auf alle Zeckenstiche anwenden zu können.

Erstelle jetzt eine Funktion namens offset_coordinate welche als Input eine x oder y-Achsenwert annimmt und eine leicht verschobene Wert zurückgibt.** Integriere die Standartabweichung der Verteilung als optionalen Parameter mit dem Namen distance und einem Defaultwert von 100.

def offset_coordinate(old, distance = 100):
    new = old + random.normalvariate(0, distance)
    return new

# die Funktion sollte so funktionieren:
offset_coordinate(x_start)

68.82755585536623

Übung 8.6

Nun ist es wichtig, dass wir unser Resultat visuell überprüfen. Im Beispiel unten wende ich die in der letzten Übung erstellte Funktion offset_coordinate() 1’000 mal auf die Dummykoordinate an. Nutze deine Funktion offset_coordinate um eine Visualisierung gemäss untenstehendem beispiel zu machen.

x_neu_list = [offset_coordinate(x_start) for i in range(1, 1000)]
y_neu_list = [offset_coordinate(y_start) for i in range(1, 1000)]

# Liste in eine Pandas DataFrame überführen
mysim = pd.DataFrame({"x" : x_neu_list, "y" : y_neu_list})

mysim.plot("x", "y", kind = "scatter")

from matplotlib import pyplot as plt
plt.axis("equal")

NameError: name 'pd' is not defined